Lumped element model

The lumped element model (also called lumped parameter model, or lumped component model) simplifies the description of the behaviour of spatially distributed physical systems into a topology consisting of discrete entities that approximate the behaviour of the distributed system under certain assumptions. It is useful in electrical systems (including electronics), mechanical multibody systems, heat transfer, acoustics, etc.

Mathematically speaking, the simplification reduces the state space of the system to a finite number, and the partial differential equations (PDEs) of the continuous (infinite-dimensional) time and space model of the physical system into ordinary differential equations (ODEs) with a finite number of parameters.

Contents

Examples

Lumped element model in electrical systems

The lumped element model of electronic circuits makes the simplifying assumption that the attributes of the circuit, resistance, capacitance, inductance, and gain, are concentrated into idealized electrical components; resistors, capacitors, and inductors, etc. joined by a network of perfectly conducting wires.

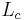The lumped element model is valid whenever L_c \ll \lambda, where L_c denotes the circuit's characteristic length, and \lambda denotes the circuit's operating wavelength. Otherwise, when the circuit length is on the order of a wavelength, we must consider more general models, such as the distributed element model (including transmission lines), whose dynamic behaviour is described by the Maxwell equations. Another way of viewing the validity of the lumped element model is to note that this model ignores the finite time it takes signals to propagate around a circuit. Whenever this propagation time is not significant to the application the lumped element model can be used. This is the case when the propagation time is much less than the period of the signal involved. However, with increasing propagation time there will be an increasing error between the assumed and actual phase of the signal which in turn results in an error in the assumed amplitude of the signal. The exact point at which the lumped element model can no longer be used depends to a certain extent on how accurately the signal needs to be known in a given application.

Real-world components exhibit non-ideal characteristics which are, in reality, distributed elements but are often represented to a first-order approximation by lumped elements. To account for leakage in capacitors for example, we can model the non-ideal capacitor as having a large lumped resistor connected in-parallel even though the leakage is, in reality distributed throughout the dielectric. Similarly a wire-wound resistor has significant inductance as well as resistance distributed along its length but we can model this as a lumped inductor in series with the ideal resistor.

Lumped element model in mechanical systems

The simplifying assumptions in this domain are:

Lumped element model in acoustics

In this context, the lumped component model extends the distributed concepts of Acoustic theory subject to approximation. In the acoustical lumped component model, certain physical components with acoustical properties may be approximated as behaving similarly to standard electronic components or simple combinations of components.

See also

External links